Veja aqui um exemplo de como interpolar dados vetoriais, trazendo-os para o formato raster usando o método Nearest neighbour, por meio do uso do python e GDAL.
Apenas lembrando que:
O GDAL é uma translator library para dados vetoriais e rasteriais, com modelos próprios para trabalhar esses tipos de dados.
Uma grande diversidade de pacotes e libraries em diversas linguagens são baseados no GDAL. Acredito que vale muito a pena saber usá-la até para entender melhor a estrutura dos dados no contexto de GIS.
O GDAL tem API para diversas linguagens, incluindo o python. A API para python pode ser consultada aqui
Porque interpolamos dados?
É uma atividade relativamente comum no dia-dia da ciência de dados. Muito comum se estivermos tratando de dados climáticos, obtidos de estações e geração de mapas para o usuário.
Como podemos entender interpolação e como ela difere de outros processos, como por exemplo, a extrapolação?
Fazendo uma rápida busca pela internet, encontramos muitos resultados que buscam de alguma maneira diferenciar esses termos na tentativa de definir o que de fato é interpolação.
Extrapolation is a way to make guesses about the future or about some hypothetical situation based on data that you already know. You’re basically taking your “best guess”. For example, let’s say your pay increases average $200 per year. You can extrapolate and say that in 10 years, your pay should be about $2,000 higher than today.
Interpolation allows you to estimate within a data set; it’s a tool to go beyond the data. It comes with a high degree of uncertainty. For example, let’s say you measure how many customers you get every day for a week: 200, 370, 120, 310, 150, 70, 90. According to that number, you should get just under 10 customers per hour (1,310 customers/ 168 hours in a week). Let’s say you staff your business 24-7 to deal with those hourly customers. You’re probably going to get zero customers at night and on the weekends, therefore wasting resources. (Note: a better way to figure out peak times is the Poisson Distribution).
(Definições retiradas dessa página aqui
Há materiais mais técnicos que podem oferecer definições e conceitos mais elaborados e completos, mas dá para entender que o processo de interpolação é algo muito corriqueiro e necessário quando lidamos com dados geoespacializados (Precisamos “distribuir” a informação ao longo da superfície para entender o que acontece!).
Especialmente quando temos algumas amostras, obtidas de coletas de campo, ou registro de sensores, etc. Não entrando no mérito de ser ou não adequado interpolar certa variável (por exemplo, devido à intensa variabilidade espacial que certos atributos de solo têm), o fato é que frequentemente precisamos recorrer a esse processo para gerar uma possível melhor compreensão sobre certa questão, ou até mesmo fornecer um produto.
Há muitos métodos de interpolação
O estudo de alguns desses métodos, e o entendimento de sua apliucação e adequação para cada caso, é fundamental.
O método nearest neighbour por exemplo, é até não considerado como interpolação por alguns autores. Isso porque o método não faz nenhum cálculo, ele simplesmente pega o valor mais próximo como ele é para preencher determinada posição.
É extremamente simples, não promove também nenhum tipo de suavização (exatamente porque não faz nenhum cálculo).
Suponha que a partir de alguns pontos extraídos aleatoriamente de uma imagem de NDVI quero fazer uma interpolação, e avaliar os resultados entre os diferentes métodos.
Os pontos extraídos (100 no total) de maneira aleatória estão dispostos da seguinte maneira:
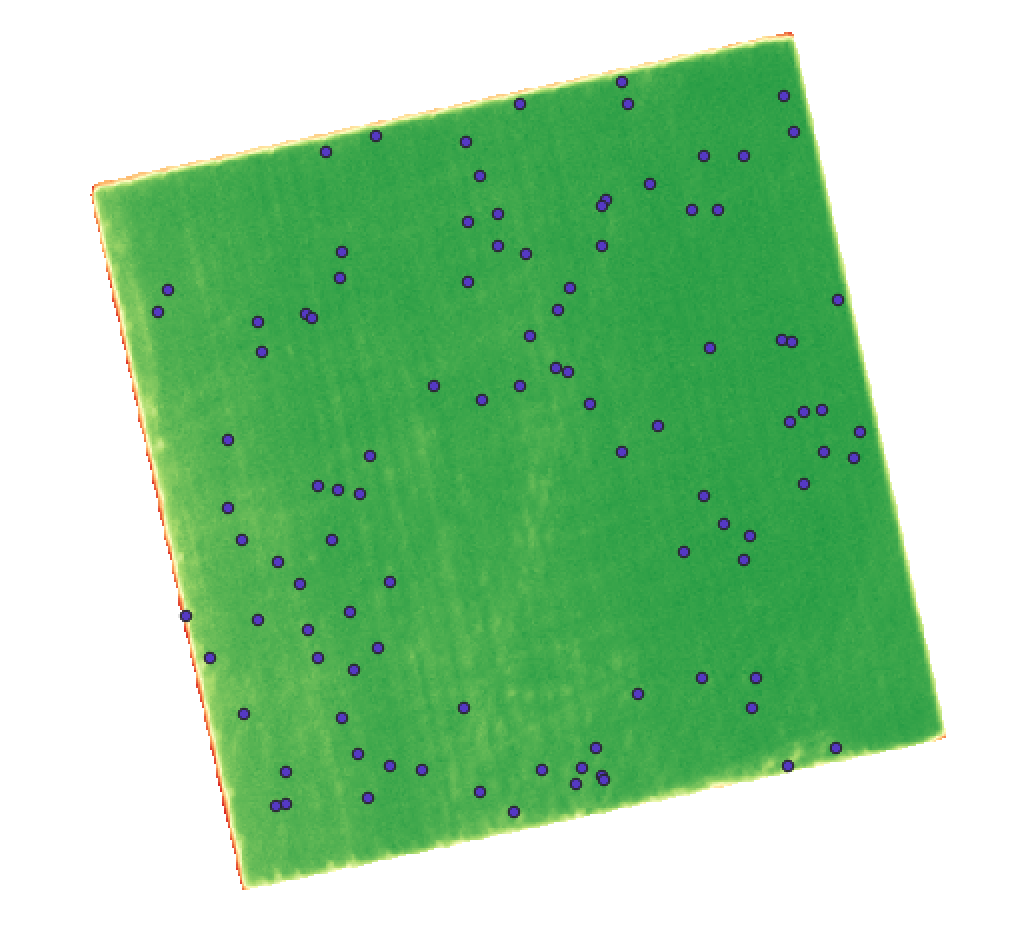
É claro que com essa distribuição heterogênea não teremos uma boa qualidade do produto final, independente do método. Mas seguindo com o objetivo de exemplificar as metodologias e compará-las.
Libraries
from osgeo import gdal
from osgeo import ogr
Dados vetoriais e ajustes
# Nearest neighbor
# atribui o valor do ponto mais próximo na elipse de busca
# janela de busca em gridding algorithms
# descrito por 3 parametros
# 1-radius1(x); 2-radius2(y); 3-angle
# (para maior detalhamento, checar página do GDAL)
# Arquivo vetorial que será o input da interpolação
pts = ogr.Open(p + 'sampled_ndvi.shp', 0)
layer = pts.GetLayer()
for field in layer.schema:
print(field.name) # checar
pts = layer = None
Nessa etapa, podemos checar o nome da coluna de atributos, que deverá ser usada na etapa seguinte.
Algoritmo NN
# algoritmo nn
nn = gdal.Grid('path_to_raster_interpolado',
p + 'sampled_ndvi.shp',
zfield = 'VALUE', # checa o nome em seu arquivo vetorial
algorithm = 'nearest')
nn = None # não esquecer de fechar
Ao checar o raster, verá que provavelmente está distante da realidade, os limites da interpolação seguem os pontos, alguns pontos quase que não são cobertos pelo arquivo final.

Você pode fazer um ajuste, para que o arquivo final após interpolação esteja de acordo com o limites (boundaries) do seu raster original (atenção, ainda não corresponderá exatamente ao raster original!)
Aqui, checo um raster modelo (o raster do qual extraí os pontos de maneira aleatória), e acesso objeto Transform para utilizar novamente.
# Mas antes, importante: Todos os inputs devem ter a mesma projeção!
# Caso eu tivesse, por exemplo, o vetor em epsg 4326 e precisasse
# mudar para o epsg do raster:
ds = gdal.Open('path_to_model_raster')
dsReprj = gdal.Warp('path_to_reproj_raster',
ds,
dstSRS = 'EPSG:4326')
ds = dsReprj = None
# Caso estejam na msma projeção, apenas continuar:
pts = ogr.Open('path_to_shp_file', 0)
layer = pts.GetLayer()
for field in layer.schema:
print(field.name)
ndvi = gdal.Open('path_to_reproj_raster')
gt = ndvi.GetGeoTransform()
ulx = gt[0] # canto superior esquerdo
uly = gt[3]
res = gt[1] # resol. espacial
xsize = ndvi.RasterXSize
ysize = ndvi.RasterYSize
# (para calcular os boundaries do raster)
lrx = ulx + xsize * res # lower right x
lry = uly - ysize * res # lower right y
ndvi = None
pts = layer = None
# e faz a interpolação por nn novamente
nn = gdal.Grid('path_to_raster_interpolado_2',
'path_to_shp_file',
zfield = 'rvalue_1',
algorithm = 'nearest',
outputBounds = [ulx, uly, lrx, lry],
width = xsize,
height = ysize)
nn = None
E agora observamos que os limites “aumentaram” um pouco, de acordo com os boundaries do raster original. Nenhum ponto encontra-se fora dos limites.

Obs: Usei como fonte para o código o canal Making Sense Remotely, que tem ótimos tutoriais de GIS para R e python. Veja aqui.