Veja aqui um exemplo de como interpolar dados vetoriais, trazendo-os para o formato raster usando o método Inverse Distance Weighting, mais conhecido como IDW, por meio do uso do python e GDAL.
Apenas lembrando que:
O GDAL é uma translator library para dados vetoriais e rasteriais, com modelos próprios para trabalhar esses tipos de dados.
Uma grande diversidade de pacotes e libraries em diversas linguagens são baseados no GDAL. Acredito que vale muito a pena saber usá-la até para entender melhor a estrutura dos dados no contexto de GIS.
O GDAL tem API para diversas linguagens, incluindo o python. A API para python pode ser consultada aqui
IDW é um método bastante popular no processo de interpolação
Esse método, assim como outros, baseia-se no fato de que pontos mais próximos tendem a serem similares entre si (por exemplo, têm maiores correlações e mais similaridades do que com pontos que estão mais longes).
No método IDW, assume-se que essa similaridade entre pontos vizinhos é proporcional à distância entre eles (definida por função que usa o inverso da distância, e o parâmetro p - a potência).
Esse método acaba sendo bastante flexível devido à essa possibilidade de ajustar o parâmetro p. Mas além disso você pode também ajustar o raio de busca do algoritmo, permitindo a delimitação de áreas para que seja feita a interpolação.
Vou usar os mesmos pontos extraídos (100 no total) de maneira aleatória e usado nos exemplos anteriores de interpolação.
Os pontos estão dispostos da seguinte maneira:
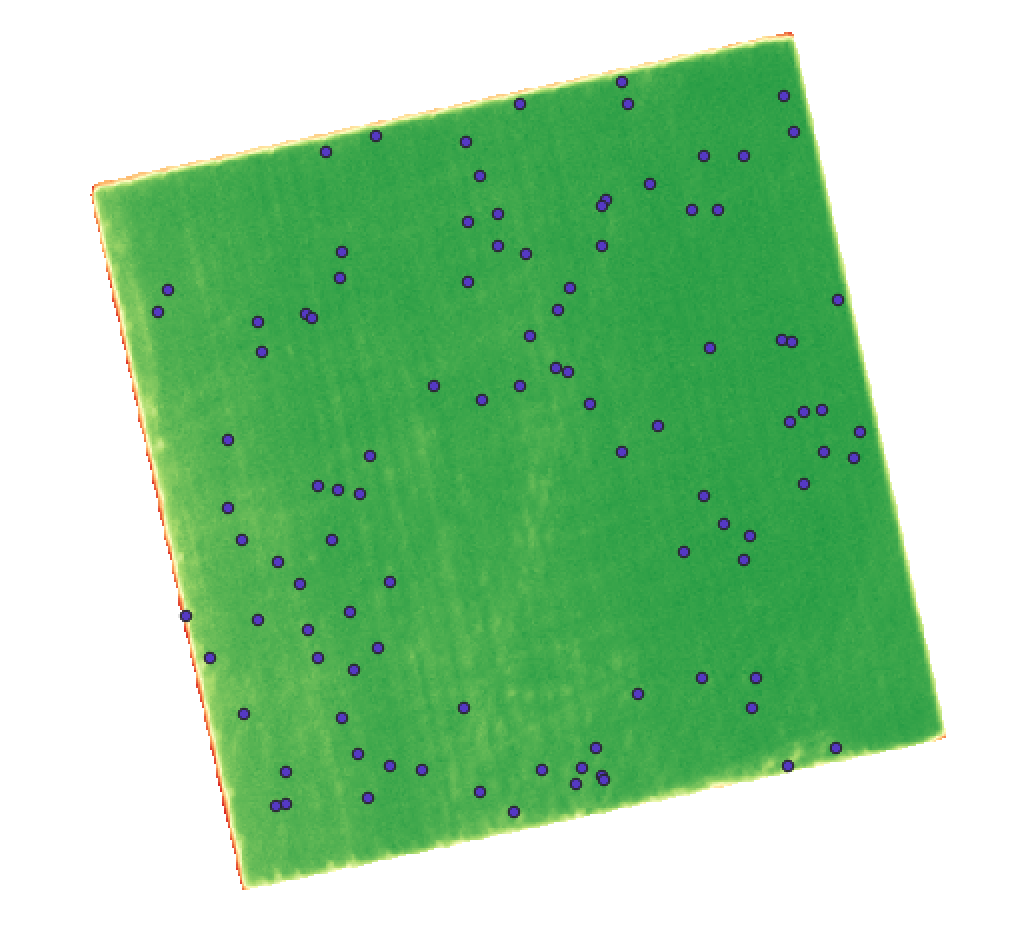
É claro que com essa distribuição heterogênea não teremos uma boa qualidade do produto final, independente do método. Mas seguindo com o objetivo de exemplificar as metodologias e compará-las.
Libraries
from osgeo import gdal
from osgeo import ogr
Dados vetoriais e ajustes
# IDW (inverse distance to a power)
# determina valores desconhecidos usando uma média ponderada de valores a partir
# de pontos conhecidos,
# assume que valores mais próximos têm maior influência do que aqueles que
# estão mais distantes
# (não precisa fornecer radius e angle values para usar uma elipse,
# pdoe apenas fornecer max_points, por ex)
# power: determina a taxa na qual o peso decresce
# w = 1 / r^p
# smooth
pts = ogr.Open(p + 'sampled_ndvi.shp', 0)
layer = pts.GetLayer()
for field in layer.schema:
print(field.name) # checar field name
Nessa etapa, podemos checar o nome da coluna de atributos, que deverá ser usada na etapa seguinte.
# Importante: Todos os inputs devem ter a mesma projeção!
# Caso eu tivesse, por exemplo, o vetor em epsg 4326 e precisasse
# mudar para o epsg do raster:
# ds = gdal.Open('path_to_model_raster')
# dsReprj = gdal.Warp('path_to_reproj_raster',
# ds,
# dstSRS = 'EPSG:4326')
# ds = dsReprj = None
# Além disso, uso informações do raster original (de onde tirei os pontos amostrais)
# para criar o arquivo interpolado
# Continuando, após de acertar projeções
ndvi = gdal.Open(p + 'mergedNDVI2.tif')
gt = ndvi.GetGeoTransform()
ulx = gt[0] # upper left corner
uly = gt[3]
res = gt[1]
xsize = ndvi.RasterXSize
ysize = ndvi.RasterYSize
# (para calcular os boundaries do raster)
lrx = ulx + xsize * res # lower right x
lry = uly - ysize * res # lower right y
ndvi = None
pts = layer = None
Até agora apenas preparamos os dados necessários, que serão usados na implementação do algoritmo de fato, a seguir.
Algoritmo IDW
# da mesma maneira que feito p/ o algoritmo Nearest Neighbour
# agora apenas mudando o algoritmo e seus parâmetros
idw = gdal.Grid(p + 'ndvi_idw',
p + 'sampled_ndvi.shp',
zfield = 'VALUE',
algorithm = 'invdist:power=3:radius1=1000:radius2=1000',
outputBounds = [ulx, uly, lrx, lry],
width = xsize,
height = ysize)
idw = None
E agora podemos ver o raster gerado, lembrando que para chegar nos limites exatos do formato do raster original deverá ser feita a operação de clip.
O resultado tem as características de uma interpolação em IDW, os chamados bull`s eyes.

Obs: Usei como fonte para o código o canal Making Sense Remotely, que tem ótimos tutoriais de GIS para R e python. Veja aqui.